一致性哈希算法
云计算与分布式存储课堂上,老师提出了这么一个问题:
在一个场景中,如果有大规模的数据集(用户主机),如何将它们分配到有限的存储节点上。另外,假设一个存储节点(服务器主机)宕机了,如何能够快速地完成数据迁移。
由此引出了一致性哈希算法。
相较于传统的哈希算法,哈希算法 hash(key) % n,其中n为节点数,因此当n发生变化,在最坏的情况下可能要所有的数据都迁移。
一致性哈希的本质是通过某个 hash 函数把 key 映射到一个很大的环形空间里。
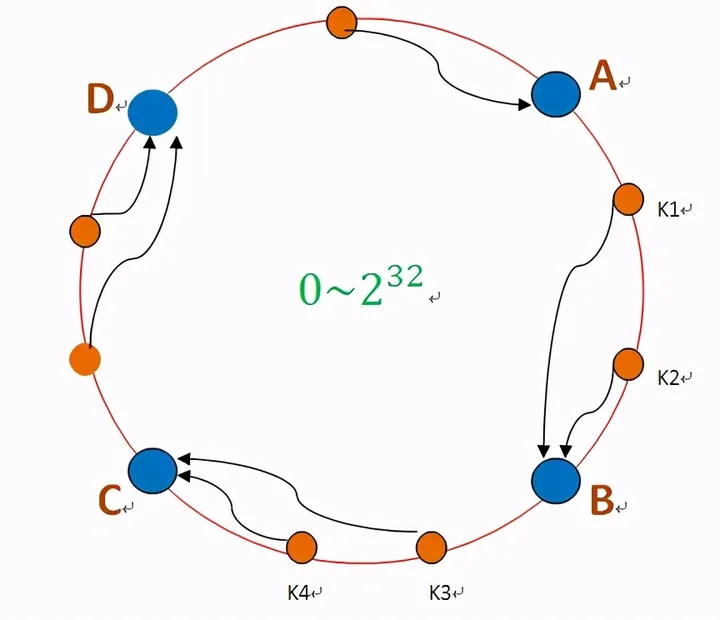
如图,存储某个数据,先计算出哈希值,然后沿着哈希环顺时针寻找到第一个存储节点。如k1和k2的存储节点是B。
如果B宕机了,就沿着哈希表继续顺时针迁移到C,存储节点B中的所有节点都会迁移到C。
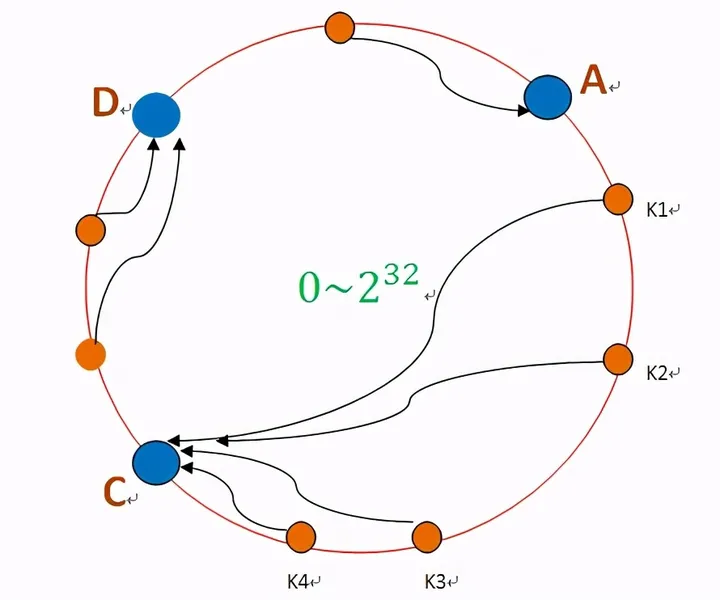
存储节点的位置同样由哈希函数得到。
但是,这里有两个问题,由于哈希环的空间通常很大,存储节点不一定能均匀的分布在哈希环上,可能会出现某一个存储节点负载过多。
另外,当某一个主机宕机,很有可能的原因是它的负载过大,然而我们如果将其数据全部迁移到某个主机,很容易导致“雪崩效应”,导致大量主机宕机。
因此,引入“虚拟节点”,一个物理存储主机生成多个虚拟主机,可以提高主机在环上的分散程度。这样以来,即使某个主机宕机,它的数据集也能很均匀地迁移到其他主机的虚拟节点上,不会造成雪崩现象。
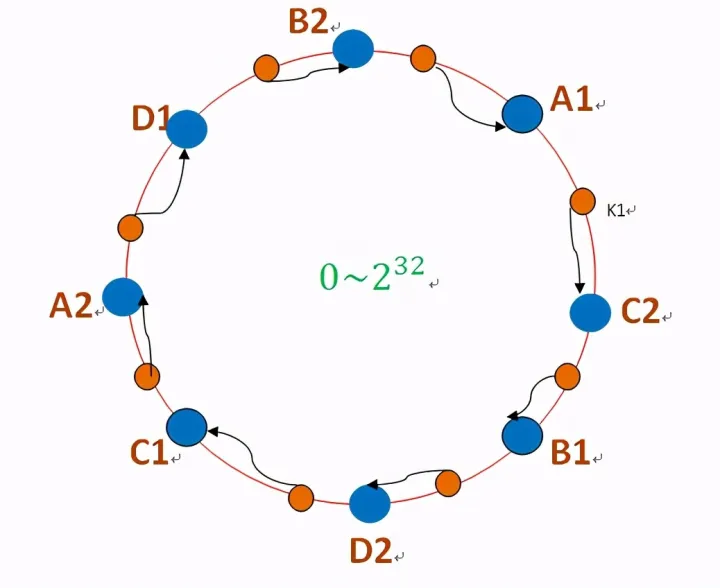
一致性哈希算法的代码演示:
#include <functional>
#include <iostream>
#include <map>
#include <random>
#include <string>
#include <vector>
// Hash函数,可以根据需求更改为其他函数,这里使用了std::hash
typedef std::function<size_t(const std::string &)> HashFunction;
// 示例哈希函数
size_t hashFunction(const std::string &key) { return std::hash<std::string>{}(key); }
// 一致性哈希类
class ConsistentHash {
private:
// 虚拟节点数量,可根据需求调整
const size_t virtualNodes;
// 哈希函数
HashFunction hashFunction;
// 圆环
std::map<size_t, std::string> hashRing;
// 物理节点负载信息,存储节点上的 IP 数量
std::map<std::string, std::vector<std::string>> nodeIPs;
public:
// 需要服务的IP地址
std::vector<std::string> ipDataset; // 将ipDataset作为类成员
// 构造函数
ConsistentHash(size_t vNodes, HashFunction func) : virtualNodes(vNodes), hashFunction(func) {}
void init(std::vector<std::string> nodes) {
for (const std::string &node : nodes) {
addNode(node);
}
for (auto &ip : ipDataset) {
getNode(ip);
}
}
// 生成模拟的 IP 地址数据集
void generateIPDataset(int dataSize) {
std::random_device rd;
std::mt19937 gen(rd());
std::uniform_int_distribution<> dis(1, 255);
for (int i = 0; i < dataSize; ++i) {
std::string ip = std::to_string(dis(gen)) + "." + std::to_string(dis(gen)) + "." +
std::to_string(dis(gen)) + "." + std::to_string(dis(gen));
ipDataset.push_back(ip);
}
}
// 添加节点到哈希环
void addNode(const std::string &node) {
for (size_t i = 0; i < virtualNodes; ++i) {
// 为每个节点创建多个虚拟节点,用不同的哈希值
std::string virtualNodeName = node + "_" + std::to_string(i);
size_t hash = hashFunction(virtualNodeName);
hashRing[hash] = node; // 虚拟节点映射到实际节点
}
}
void resetRing() {
nodeIPs.clear(); // 清除负载记录
// 重新分配 IP 地址到虚拟节点
for (auto &ip : ipDataset) {
std::string selectedNode = getNode(ip);
}
}
// 删除节点及其对应的所有虚拟节点,并重新分配 IP 地址
void removeNode(const std::string &node) {
std::vector<size_t> virtualNodeHashesToRemove;
// 找到需要移除的节点对应的虚拟节点
for (auto it = hashRing.begin(); it != hashRing.end();) {
if (it->second == node) {
virtualNodeHashesToRemove.push_back(it->first);
it = hashRing.erase(it);
} else {
++it;
}
}
// 从节点负载信息中移除节点
nodeIPs.erase(node);
// 重新分配需要移除节点上的虚拟节点对应的 IP 地址到其他节点
for (size_t hash : virtualNodeHashesToRemove) {
for (auto &pair : nodeIPs) {
std::string newNode = pair.first;
if (newNode != node) {
size_t newHash = hashFunction(newNode + "_" + std::to_string(hash));
hashRing[newHash] = newNode;
}
}
}
}
// 根据给定的键查找对应的节点
std::string getNode(const std::string &key) {
size_t hash = hashFunction(key);
auto it = hashRing.lower_bound(hash);
// std::cout << it->first << std::endl;
if (it == hashRing.end()) {
// 如果超出了范围,返回第一个节点(环形结构)
it = hashRing.begin();
}
// 将 IP 添加到所选节点
std::string selectedNode = it->second;
nodeIPs[selectedNode].push_back(key);
return selectedNode;
}
// 获取节点负载信息,按照 IP 数量计算负载百分比
void statisticPerf() const {
std::map<std::string, double> loadPercentages;
size_t totalKeys = 0;
// Calculate total number of keys (IPs) on the entire hash ring
for (const auto &nodeIP : nodeIPs) {
totalKeys += nodeIP.second.size();
}
// Calculate load percentage for each node
for (const auto &nodeIP : nodeIPs) {
double percentage = (static_cast<double>(nodeIP.second.size()) / totalKeys) * 100.0;
loadPercentages[nodeIP.first] = percentage;
}
// Output node load percentages
std::cout << "Node Loads (%):\n";
for (const auto &load : loadPercentages) {
std::cout << load.first << ": " << load.second << "%" << std::endl;
}
}
};
int main() {
// 创建一致性哈希对象并传入MurmurHash3作为哈希函数
ConsistentHash consistentHash(1000, hashFunction); // 构造哈希环,设置虚拟节点个数
// 生成模拟的 IP 地址数据集
consistentHash.generateIPDataset(100000); // 生成模拟 IP 地址
// 初始化存储节点,分配IP到存储节点
std::vector<std::string> nodeList = {"node1", "node2", "node3", "node4"};
consistentHash.init(nodeList);
consistentHash.statisticPerf();
// 增加存储节点,重新分配所有IP地址
consistentHash.addNode("node5");
consistentHash.resetRing();
consistentHash.statisticPerf();
// 删除存储节点,重新分配该节点上的IP
consistentHash.removeNode("node3");
consistentHash.statisticPerf();
return 0;
}
代码中为了负载均衡,addNode后,会重新分配数据集到所有存储节点;
removeNode方法,只分配该待删除节点上的数据。
ConsistentHash consistentHash(1, hashFunction);
consistentHash.generateIPDataset(100000);
即不设置虚拟节点,可以发现负载情况非常不均衡
Node Loads (%):
node1: 22.478%
node2: 2.843%
node3: 49.858%
node4: 24.821%
…
ConsistentHash consistentHash(1000, hashFunction);
consistentHash.generateIPDataset(100000);
由于哈希函数的范围比较大,这里多设置几个虚拟节点和数据集,负载均衡。
–初始情况– Node Loads (%): node1: 24.96% node2: 24.93% node3: 25.333% node4: 24.777% –插入存储节点– Node Loads (%): node1: 19.978% node2: 19.427% node3: 19.634% node4: 20.024% node5: 20.937% –删除存储节点– Node Loads (%): node1: 24.8588% node2: 24.1732% node4: 24.916% node5: 26.0521%